Complex Valued Neural Networks might be the future of Deep Learning

Evaluating a possible future Machine Learning paradigm

11 min readDec 18, 2023

Executive Summary-

Complex Valued Neural Networks (CVNNs) have the potential to accelerate AI adoption in many high-impact fields. They offer many advantages over traditional Real-Valued Neural Nets (RVNNs)

Estimated Market Size: USD 2.3 Billion (next 3–5 years) and 13 Billion over the next decade (based on rough calculations).

Time frame: 2–4 years for the first major breakthrough, 3–8 years for a major product (unicorn). 7–11 years for this to become mainstream.

The fields where these can be implemented most readily are: Signal Communications; Healthcare (both medical image and ECG); Deep Fake Detections; and Acoustic Analysis for Industrial Maintenance and expansion. For these fields, the present technology is enough, and the challenge is to adapt AI to these fields. Good betas can be created within one year, after which some refinement will be needed.

For a more detailed overview of the areas we use CVNN currently

More moonshot investments include: Hardware for CVNNs; the detection of AI Generated Content; Data Compression; Data Quality Analysis; and High Performance Computing. These will require some dedicated R&D to create market-ready solutions. Their utility in Quantum Computing also came up in my research, but given my lack of knowledge in this area, I will not make any comments.

optical computing platforms that encode information in both phase and magnitude can execute complex arithmetic by optical interference, offering significantly enhanced computational speed and energy efficiency…Strong learning capabilities (i.e., high accuracy, fast convergence and the capability to construct nonlinear decision boundaries) are achieved by our complex-valued ONC compared to its real-valued counterpart.
-“An optical neural chip for implementing complex-valued neural network”

Why CVNNs- Complex numbers work very well for phasic data. They show encouraging results in raw performance, expressiveness, stability, and generalization. CVNNs can also be implemented without gradients, increasing their utility to more non-traditional data types. They are presently held back by high unit costs, lack of research, and inherently… complexity (yes, I’m proud of that). If these issues are resolved, they will accelerate the adoption of Deep Learning in many high-impact fields.

If this interests you, let’s proceed by digging into the results of the investigation. I will cover the theory in more detail, evaluating the results of various experiments to present their potential for adoption in the aforementioned use cases.

A massive thank you to our main man Andrew Gillies for his suggestion of including this section for longer articles. I’ll try to have these in more articles, for days you’re too busy to read the whole thing.

Join 150K+ tech leaders and get insights on the most important ideas in AI straight to your inbox through my free newsletter- AI Made Simple

Introduction

Neural Networks have been instrumental in adapting Machine Learning to a wide variety of tasks in AI. Their versatility with unstructured data allows their adoption in many problems. Recently, I came across a very interesting paper, “Generalized BackPropagation, Étude De Cas: Orthogonality, which shared the following-

This paper introduces an extension of the backpropagation algorithm that enables us to have layers with constrained weights in a deep network. In particular, we make use of the Riemannian geometry and optimization techniques on matrix manifolds to step outside of normal practice in training deep networks, equipping the network with structures such as orthogonality or positive definiteness… We will see that on the Cars196 Krause et al.(2013) dataset, replacing the fc7 layer of the VGG-M Simonyan and Zisserman (2014) by orthogonal layers leads to boosting the classification accuracy from 77.5% to 82.0%, while the number of parameters of fc7 is reduced from 16.7M to 745K.

Given these goated numbers, I had to dig into this in more detail. Much of the contributions here are enabled by the usage of orthogonality and a type of gradient descent called the Reinmann Gradient Descent. The latter is interesting enough for a dedicated breakdown, but my attention was pulled towards the former. A while back, I’d covered Hybrid Convolutional Neural Networks- CNNs that replaced lower levels of convolutions with a complex function- and that was the first time I came across orthogonality and its potential power-

The decision boundary of a CVnn consists of two hypersurfaces that intersect orthogonally (Fig. 7) and divides a decision region into four equal sections. Furthermore, the decision boundary of a 3-layer CVnn stays almost orthogonal [27]. This orthogonality improves generalization. As an example, several problems (e.g. Xor) that cannot be solved with a single real neuron, can be solved with a single complex-valued neuron using the orthogonal property

This had me thinking about the use of complex numbers in AI. And my investigation into them was fascinating. To get deeper into it, let’s first look into why CVNNs are absolute units.

Why Complex numbers?

To simplify very difficult math, complex analysis is built around the unit circle. This cyclical nature allows it to adapt very well to phasic data: images, signals, etc.

The way I see it, the phasicness of Complex networks gives them a very different nature to real-valued networks. Their ‘perception of the data’ and subsequent decision boundaries are very different since they are built around the unit circle (note this is just my hypothesis).

Fig. 1. Geometric Interpretation for discrete-valued MVN activation function

As demonstrated in the excellent, A Survey of Complex-Valued Neural Networks, we see CVNNs thrive w/ periodic, wave-like (phasic) data-

Ultimately, they’re able to encode more information than real-valued data (this is called their expressiveness).

Their weirdness also leads to some very interesting extensions. We can build gradient-free neural networks. “For a single neuron, weight correction in the MVN is determined by the neuron’s error, and learning is reduced to a simple movement along the unit circle.” Take a simple complex neural network with multi-valued neurons (MLMVN) shown below-

For this, we implement gradient-free learning as follows-

“Ckj is the learning rate for the kth neuron of the jth layer. However, in applying this learning rule two situations may arise: (1) the absolute value of the weighted sum being corrected may jump erratically, or (2) the output of the hidden neuron varies around some constant value. In either of these scenarios, a large number of weight updates can be wasted. The workaround is to instead apply a modified learning rule which adds a normalization constant to the learning for the hidden and input layers. However, the output layer learning error backpropagation is not normalized. The final correction rule for the kth neuron of the mth (output) layer is”

No gradients →no getting stuck in local minima.

The non-gradient-based approach is special since it allows us to work w/ discrete input/activation functions, possibly even combining them with continuous ones. Some of you will remember my earlier investigation, How to take back control of the internet. I see this being a great addition to the ideas discussed about breaking website blockers and signal jammers.

Fig. 4 **A complex-valued layer for classification of dataset Iris**. The ONC is reconfigured with the complex-valued weight matrix trained for Iris task. The complex-valued neuron outputs are measured and displayed in two-dimensional Cartesian diagrams, as in a–c. The three shown cases are trained by three respective targets: phase only (φ1, φ2, φ3), magnitude only (ρ1, ρ2, ρ3) and their combinations (ρ1, (ρ2, φ1), (ρ2, φ2)). The circle markers are the validation results of training dataset while the triangle markers are those of the blind test instances. Data points which were wrongly predicted in the blind test are circled in red. It is shown by validation results that the optical chip identifies successfully the three species from the known data. While from testing results, we learn that the generalized model also fits well to unknown data.

All of this is very encouraging. So why haven’t we seen CVNNs more often? Why are these not mainstream? Let’s talk about some of the challenges holding them back from mass adoption.

the authors considered the issue of requiring long sequences for training, which results in a lot of wasted channel capacity in cases where nonlinearities associated with the channel are slowly time varying. To solve this problem, they investigated the use of CVNN for adaptive channel equalization. The approach was tested on the task of equalizing a digital satellite radio channel amidst intersymbol interference and minor nonlinearities, and their approach showed competitive results. They also pointed out that their approach does not require prior knowledge about the nonlinear characteristics of the channel.

Risks-

Firstly, CVNNs are held back by a lack of R&D into optimizations. Given that we tend to think along the real plane, most of the optimizations written implicitly assume real-valued data. This holds us back when it comes to performance and implementation. People often underestimate the impact that the underlying platforms can have on AI. Trying to build complex-valued solutions on top of real-valued frameworks will lead to very high overhead and constant bugs. The results will be a costly and confused mess, or as the Britishers call it- Chelsea FC.

To enable CVNNs, we would need some dedicated infrastructure that takes advantage of their quirks. This was overlooked, but fortunately, this is changing. Peep the “An optical neural chip for implementing complex-valued neural network” which drops some serious heat in enabling a more bottom-up development of CVNNs. The authors “highlight an optical neural chip (ONC) that implements truly complex-valued neural networks” w/ superior learning and efficiency.

Fig. 1 The composition of complex-valued coherent optical neural network. a **An optical neural network is composed of an input layer, multiple hidden layers and an output layer**. In our complex-valued design, the light signals are encoded and manipulated by both magnitude and phase during the initial input preparation and network evolution. b The schematic of the ONC in implementing complex-valued networks. The input preparation, weight multiplication and coherent detection are all integrated onto a single chip. The division and modulation of the light signals (i1–i6) are realized by the MZIs marked in red. The green marked MZI separates the reference light that will later be used for coherent detection. The MZIs used to implement the 6 × 6 complex-valued weight matrix are marked in blue. The remaining grey marked MZIs are used for on-chip coherent detection. c The workflow of the ONC system. A coherent laser at 1550 nm is used to generate signal light and reference light. The signal light on each path is modulated by its magnitude and phase according to the machine learning (ML) task. The weighted sum operation is accomplished passively through light inference. The measurement results are sent to the electrical interface for processing, including the application of activation function and the calculation of cost function. The ONC chip are then reconfigured accordingly by the updated weight matrices

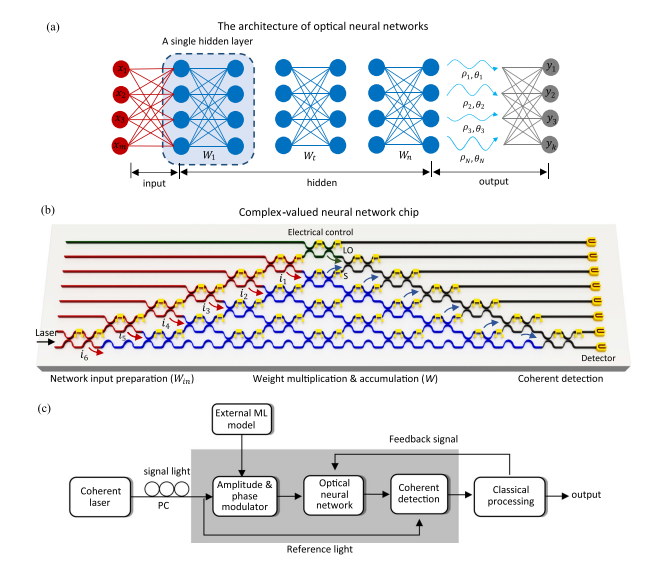
They show some great results, dominating Iris (shared earlier) and the logic gate task-

Fig. 3 A single complex-valued neuron for logic gate task. a The diagram of a complex-valued neuron and its on-chip implementation. The neuron output is the weighted sum of the input (e.g., x1R + jx1I, where the footnote R/I represents the real and imaginary part, respectively) and complex weights (e.g., w1R + jw1I), after being processed by an activation function f. The bias is implemented with an additional constant input weighted by a trainable complex-valued weight (i.e., bR + jbI). The weight matrix is decomposed to the phase shift values (θi and ϕi ) on chip. b The training process of NAND gate and c The training process of XOR gate. 10 iterations are conducted and recorded for each logic gate. The quadrants representing logical 0 are painted blue and those representing logical 1 are painted pink. Being processed by a complex-valued neuron, each of the four possible combinations of logical inputs converges from a random starting point to the expected end point, via a continuous modulation of magnitude and phase rotation.

The ONC and CVNN also show strong adaptation to non-linearities. This is most interesting to me, since the ability to handle non-linearity is what made Deep Learning. Take a look at the difference in boundaries created by the real and complex model.

All of this combines to a pretty significant difference in results-

So far a pretty great start, but there is another problem with CVNNs. Their superior expressiveness also has a downside- “Compared to real-valued parameters which use single real-valued multiplication, complex-valued parameters will require up to four real multiplications and two real additions.” This would already be very expensive, but on top of this, we see that CVNNs are also hard to regularize. And finally, “in applications involving long sequences, gradient backpropagation requires all hidden states values to be stored. This can become impractical given the limited availability of GPU memory for optimization.” This might be solved since “the inverse of the unitary matrix is its conjugate transpose, it may be possible to derive some invertible nonlinear function with which the states can be computed during the backward pass. This will eliminate the need to store the hidden state values” but this has to be solved.

All of these additional costs mean that when evaluating results, comparisons b/w parameters size of an RVNN and CVNN are not as straightforward as b/w 2 RVNN. Even if CVNNs lead to huge reductions in model size for comparable performance, they might still end up with higher costs. We can get around this with good engineering ( the use of a fixed function in the Hybrid Neural Network is a good example), but this is something to be careful about.

The resulting network is called Complex Shearlets Network (CoShNet). It was tested on Fashion-MNIST against ResNet-50 and Resnet-18, obtaining 92.2% versus 90.7% and 91.8% respectively. The proposed network has 49.9k parameters versus ResNet-18 with 11.18m and use 52 times fewer FLOPs. Finally, we trained in under 20 epochs versus 200 epochs required by ResNet and do not need any hyperparameter tuning nor regularization.
-If you can drop numbers like this, you’re fine.

Intelligent design is the bedrock of all good Machine Learning, but this becomes even more important when it comes to CVNNs since they are so much stranger.

Lastly, the hurdle stopping mass adoption of CVNNs is their inherent complexity. This might seem like a dumb thing- but ideas live and die by their ease of comprehension and use. Since CVNNs have a high barrier to entry and a steep learning curve, it can deter people from building on and around them. I’ve spent 2–3x the time on this piece than I have on any other, and I still have a long way to go to get this on par with my other skills. This will be hard to tackle since technologies really start to find their place after adoption (which is why Open Source is so good). The complexity of CVNNs can kill them before they get started.

On the flip side, this also provides a fantastic moat. If you can develop solutions around CVNNs, then it’s not something that your competitors can replicate easily. I’m generally skeptical of AI Models/Techniques being a significant USP, but this would be a rare exception. CVNNs are distinctive enough to where their benefits can’t be copied easily. While their complexity might deter their adoption in many fields, challenges where they have already been used successfully, and their adjacent problems, are great places to start working on them for quicker wins. In those fields, the existing developments need to be molded to the data/processes on hand. And if you have the risk appetite to invest in a longer-term, riskier project, then the moonshot ideas described earlier would be a great place to start.

This simulation has some issues that nerf RVNNs so don’t take it at face value, but it does demonstrate potential

If you’re looking for a resource to get started with CVNNs, “Theory and Implementation of Complex-Valued Neural Networks” is the resource for you. I will be covering more on CVNNs as I learn/experiment more, so keep your eyes peeled. As always, if you have any insights to share into this, it would be much appreciated.

If you liked this article and wish to share it, please refer to the following guidelines.

That is it for this piece. I appreciate your time. As always, if you’re interested in working with me or checking out my other work, my links will be at the end of this email/post. And if you found value in this write-up, I would appreciate you sharing it with more people. It is word-of-mouth referrals like yours that help me grow.

If you find AI Made Simple useful and would like to support my writing- please consider becoming a premium member of my cult by subscribing below. Subscribing gives you access to a lot more content and enables me to continue writing. This will cost you 400 INR (5 USD) monthly or 4000 INR (50 USD) per year and comes with a 60-day, complete refund policy. Understand the newest developments and develop your understanding of the most important ideas, all for the price of a cup of coffee.

Become a premium member